基于Matlab HDL Coder的8x8实矩阵QR分解
点我下载,使用Matlab 2018b打开。
QR分解是计算机视觉以及机器学习中重要的矩阵求逆方法。它可以将矩阵分解成一个正交矩阵Q与一个上三角矩阵R的积。一般来说,QR分解有三种方法:1. Householder transformations,2. Givens rotation,3. Gram-Schmidt orthogonalization。其中Matlab的qr()函数使用的是方法1,此处我们应用方法2来分解矩阵,方法3是一般教材中介绍的常规方法。
P.S. 实现8x8实矩阵是因为在我RANSAC的项目中需要固定实现8x8矩阵的求逆,这个基于循环的算法可以很容易的拓展到其他大小的矩阵上去,但并不适用于未知大小矩阵的分解。 本文对基于Givens旋转的QR分解原理不做介绍,具体可见一下链接:
一下贴出用于验证的matlab代码


Givens旋转的本质上就是计算两个向量夹角的sin和cos函数,因此,我们选取DSP HDL工具包中的优化CORDIC模块(Complex to Magnitude-Angle HDL Optimized)来计算,因此图1中Givens函数的Simulink模块设计如下:
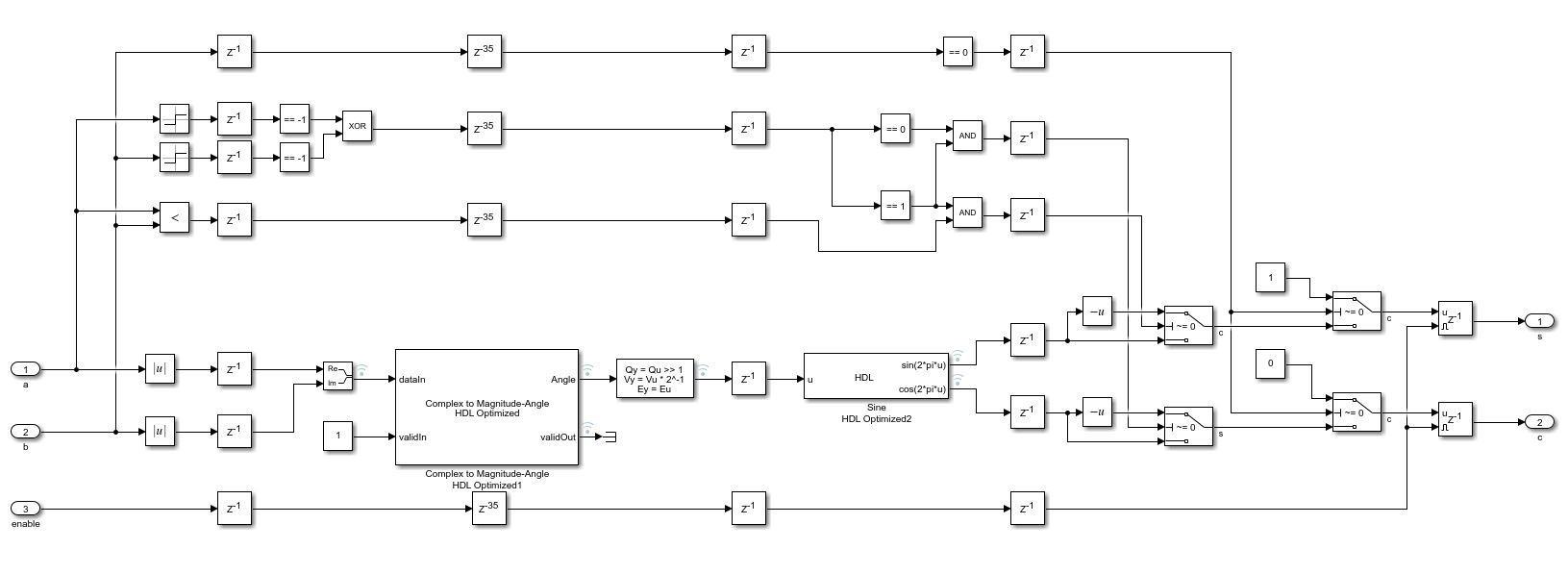
由于G矩阵只有4个非零值,所以在嵌套循环中,Q和R的每次只需要更新两行/列,其余则保持不变。我们自需要每次读出需要更新的行/列,与2x2的sub G矩阵相乘即可,如下图所示:
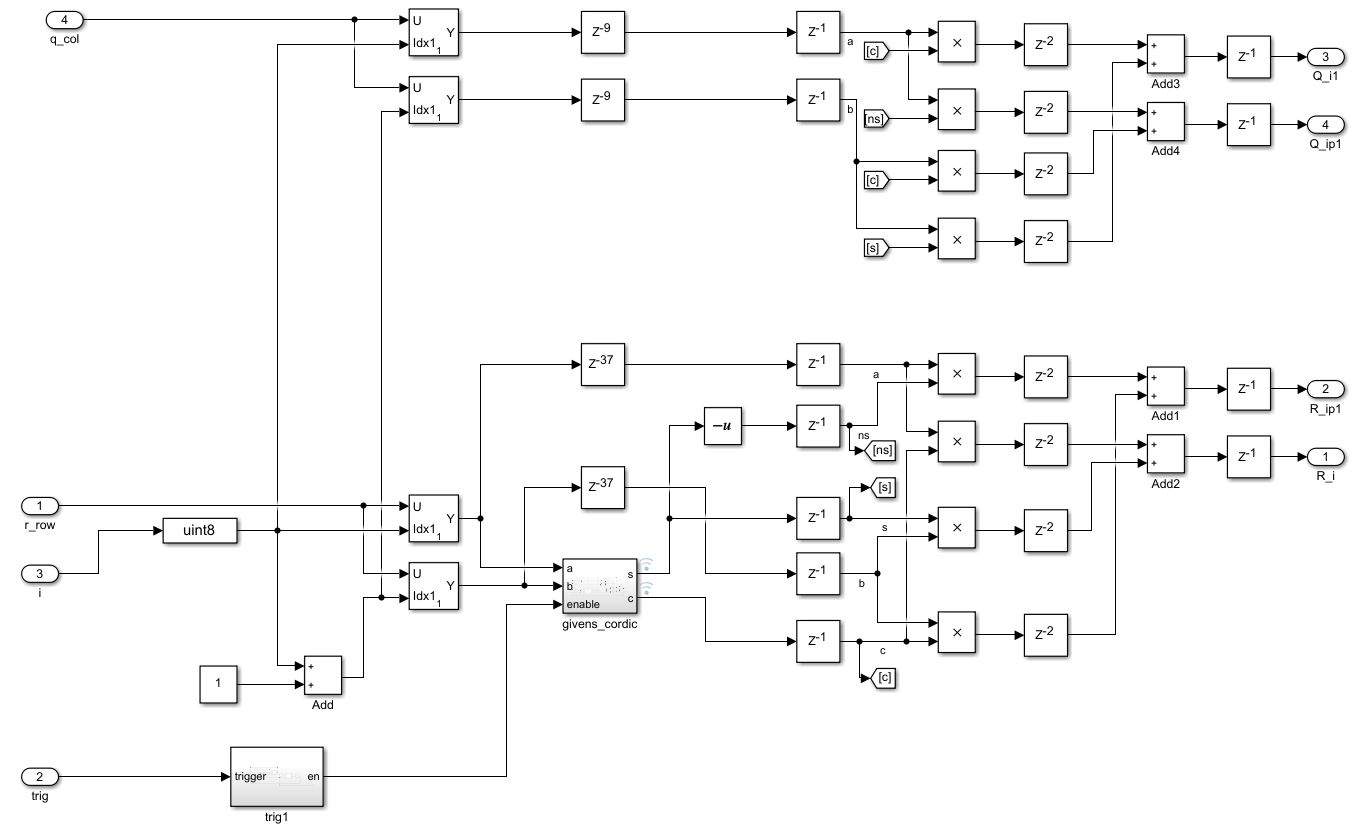
至此,基于Givens的QR分解主要功能模块已经设计完成,我们进行剩下的控制模块设计。QR分解的外部接口如下:
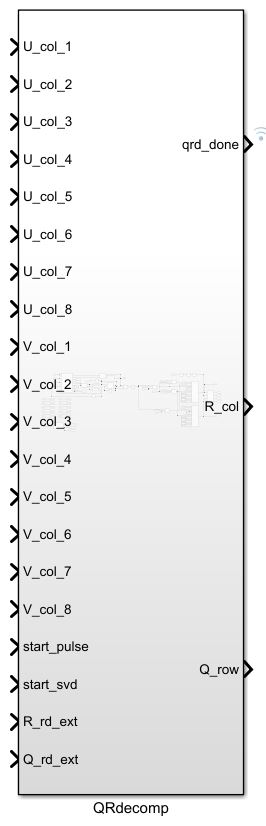
U_col_?,V_col_? - Q和R分量load接口
start_pulse - 分解完成后读取开始信号
start_svd - QR分解开始信号
R_rd_ext,Q_rd_ext - 分解完成后QR矩阵读取address
R_col,Q_row - 分解完成后QR矩阵输出
qrd_done - 分解完成信号
FSM用来控制每一步的进行。首先FSM在idle状态,当外界将待分解矩阵U和单位矩阵V装载进QR分解模块之后,将start_svd信号置1,开始QR分解(请原谅我没有把svd改成qr,我直接把svd分解的状态机拿过来改改用了)。然后FSM进入read状态读取Givens矩阵计算所需要的R分量,当计算完成后FSM进入update状态来更新Q和R矩阵。如果循环完成,则回到idle状态等待下一轮分解,否则回到read状态读取R对应分量。FSM设计推荐使用matlab function模块,具体设计参见附件模块中FSM。
嵌套计数器设计没有太多好说的,直接上图:
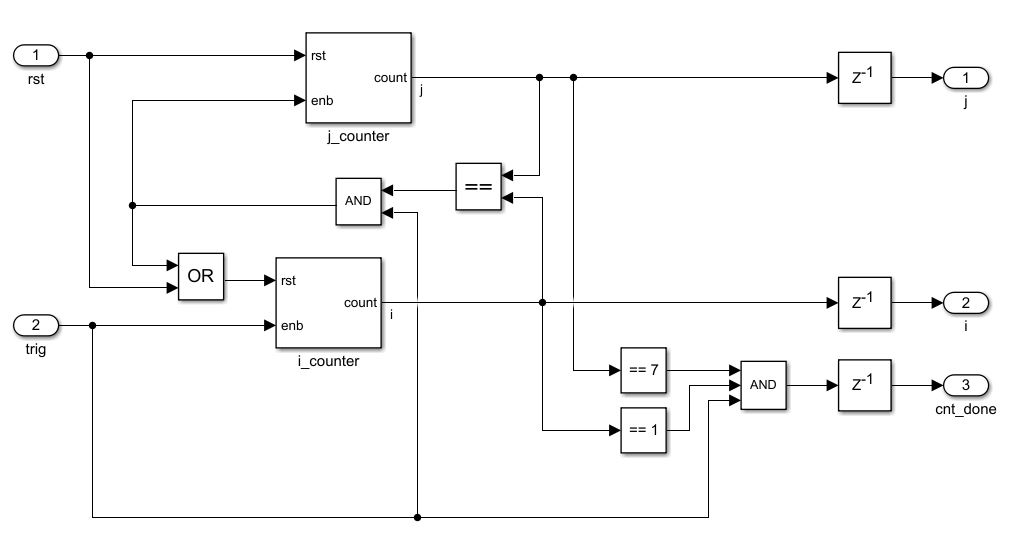
为了设计方便,我们将Q按行分别存储在8个RAM中,R按列分别存储在8个RAM中。
至此,QR分解模块已经设计完成。从性能上来看,完成一次8x8的实矩阵分解需要(1+7)*7/2=28次循环,通过logical analyzer的仿真,一共需要约1500个时钟周期。此设计的不足之处在于一些trigger的添加,比如QRdecomp/Subsystem/trig1以及与其类似的模块,这是由于对hdl coder模块功能理解不到位引起的(Enabled Delay和Unit Delay Enabled Synchronous,以后会有这两个模块的讲解)。
后话:一年前我是极其抵制使用金主爸爸的HDL Coder和Vision HDL工具包的,因为学习曲线陡峭,Community太小等原因,但是习惯就会发现这个工具实在太好了,彻底摆脱了代码的编写,可以把精力放在算法本身,并且debug比起其他HLS工具方便了很多。对于初学者建立硬件思维很有益处~